Phân tích thiết kế giải thuật
Phân Tích thiết kế Giải Thuật
I Giới thiệu
+ thuật toán:
1, kn: 1 loạt bước thực hiện bài toán( để từ input=> ouput đúng)
2, tc: chính xác, rõ ràng, khách quan, phổ dụng, kết thúc
3, bd: NN tự nhiên, sơ đồ khối, giả mã(phải mô tả đk cả input,output)
4, chất lượng bd: đúng; đơn giản; dễ cài đặt
5, Chứng minh tính đúng đắn: pp lý thuyết, thực nghiệm
6, Tính hiệu quả: thời gian, bộ nhớ, độ chính xác
+ Đánh giá độ phức tạp:
1, độ tăng của hàm: ham O (lớn) : tc: quy tắc cộng, quy tắc nhân
2, độ .. thời gian: hàm f(n): đếm số phép toán cơ bản: gán, so sánh,.. ( n là kích thước dữ liệu đầu vào): độ phức tạp là hàm chặn trên O của nó
+ Lớp P: lớp các bt giải đk bằng tg đa thức
+ Lớp NP: ......... kiểm tra tính đúng của lời giải bằng tg đa thức
-> những bài toán NP có thể là bt P được không?
+ 1 số quy tắc đánh giá: quy tắc cộng( max( 2 hàm)), quy tắc nhân( tích độ phức tạp 2 hàm), phân tích câu lệnh,,,,
+ Phương pháp đánh giá:
1 phân tích trực tiếp các đoạn mã (đếm , đếm, đếm)
=> TH không đếm đk rõ ràng ta sẽ tính TH xấu nhất
2 .............. lý thuyết
3 ............. thực nghiệm
2: thực hiện 2 việc: cm tính đúng, cm tính hiệu quả(****)
+ ví dụ: phương pháp Merge sort : sử dụng Tree để phân tích
3 thực nghiệm
+ chương trính hóa thuật toán
+ các lệnh đếm các phép toán
+ chạy chương trình trên nhiều bộ DL sẵn có
=> mỗi bộ ghi lại kết quả=> thống kê
Bài 3: Thiết kế thuật toán
1 Kn: là module hóa bài toán ban đầu thành các vấn đề nhỏ, cố gắng giải quyết tốt các vấn đề nhỏ đó => gom => giải quyết bt lớn
2 Một số kỹ thuật thiết kế
+ Chia để trị: chia thành đoạn hoặc bài toán nhỏ hơn
+ Tham lam: Chọn phương án tốt hiện thời(tốc độ nhanh, nhưng..)
+ Quy hoạch động: nhanh, kq tối ưu nhưng bộ nhớ lớn
+ Quay Lui: thử => sai => sủa
+ Nhánh cận: bc là quay lui + đánh giá cận và cắt bớt nếu ko cần
3 Tối ưu thuật toán
+ tối ưu thuật toán + thay đổi cấu trúc dữ liệu
+ Thay đổi kỹ thuật, công nghệ
+ tối ưu vòng lặp
Bài 4: chia để trị
Ý tưởng: chia bài toán => các bt con độc lập( về biên dữ liệu) vs nhau, giải bt con theo cùng 1 cách thức=> tổng hợp lại
1 Tìm kiếm nhị phân
+ Input: mảng A có n phần tử đã được sắp xếp theo thứ tự tăng dần, tìm phần tử có giá trị = X trong mảng =>
+ Output: k=-1 nếu không tìm thấy,,, 1<=k<=n nếu tìm thấy
+ Ý tưởng: lấy k= (left + right)/2 kiểm tra A[k] = X return k; nếu A[k]> X thì tiếp tục chia trên mảng left-> k-1; A[k]<X : tiếp tục chia trên: k+1 đến right
+ Cài đặt:
=> độ phức tạp O(log2(n))
2 Bài toán tìm Max và min
+ Input: mảng A có n phần tử
+ Output: giá trị lớn nhất, nhỏ nhất trong mảng A
+ Ý tưởng: chia đôi mảng A, tìm min, max trên mỗi nửa, rồi tổng hợp lại,, nếu mảng còn 1 phần tử thì min=max=phần tử đó
+ Cài đặt:
=> độ phức tap: O(n) (không giảm đk độ phức tạp)
3 Bt Merge Sort
+ Input: mảng A có n phần tử
+ Output: mảng A có n phần tử đã được sắp xếp tăng dần
+ Ý tưởng:
nếu có 2 dãy a,b đã đk sắp xếp=> trộn thành dãy c đk sắp xếp
chia nhỏ mỗi dãy chỉ còn 1 phần tử => trộn lại vs nhau
+ Cài đặt mergesort:
+ Cài đặt merge
=> độ phức tạp O(nlog(n))
4 Quick Sort
+ Input: mảng A có n phần tử
+ Output: mảng A đã được sắp xếp tăng dần
+ Ý tưởng: lấy mỗi phần tử và chuyển nó đến vị trí đúng
+ Cài đặt phân đoạn Partition :
Chọn phần tử chôt x:
• Duyệt từ vị trí tiếp sang phải tìm vị trí phần tử đầu tiên >= x, i• Duyệt từ phải sang trái, tìm vị trí phần tử đầu tiên <x, j• Nếu i<j thì hoán đổi vị trí• Tiếp tục đến lúc j<i
+ Cài đặt quicksort:
5 Bài toán nhân số nguyên lớn
+ Input: 2 số nguyên lớn x,y có n chữ số
+ Output: số nguyên lớn z = x.y
+ Ý tưởng:
=> độ phức tạp O(n^2) không nhanh hơn bình thường
+ Ý tưởng thuật toán Karatsuba
=> độ phức tạp O(nlog2(3))
+ Cài đặt karatsuba
6 Nhân ma trận
+ Input: 2 ma tran X(m,n) và Y(n,p)
+ Output: ma trận Z= tích của X và Y
+ Ý tưởng: chia X thành 4 mt con A,B,C,D ; Y thành 4 mt con E,F,G,H
=> Strassen: đặt
P1= A(F-H) P2= (A+B)H P3= (C+D)E P4= D(G-E)
P5= (A+D)(E+H) P6= (B-D)(G+H) P7= (A-C)(E+F)
7 Dãy con lớn nhất
+ Input: mảng A[1...n]
+ Output: mảng A[p...q] có trọng lượng( tổng giá trị các pt) lớn nhất, p-> q là liên tiếp 1<=p<=q<= n
+ Ý tưởng: chia mảng A thành 2 mảng đều: AL, AR
tính WL: trọng lượng (dãy con) max thuộc mảng AL
WR: trọng lượng (dãy con) max thuộc mảng AR
WM: trọng lượng (dãy con) max thuộc mảng AL,AR xuất phát tại điểm chính giữa AL ,AR => Max= Max(WL,WR,WM)
+ Cài đặt:
=> độ phức tạp O(nlog(n))
8 Tính lũy thừa
+ Tính a^n với a,n là số nguyên ko âm
+ Ý tưởng:
=> độ phức tạp O(log(n))
+ cài đặt:
9 Hoán đổi phần tử mảng
+ Input: mảng A có n phần tử
+ Output: mảng A sau khi chuyển m phần tử đầu về cuối với đk không dùng mảng phụ
+ Ý tưởng:
1, Nếu m=n-m: hoán đổi 2 mảng có độ dài bằng nhau
2, Nếu m<n-m: .............. m pt đầu vs m pt cuối => còn A[1..n-m]
cần chuyển đúng vị trí: tt hoán đổi m pt đầu vs phần còn lại
3, Nếu m>n-m: ............(n-m) phần tử đầu về cuối->.A[n-m+1...n]
cần...........................: ta hoán đổi (n-m) pt đầu vs phần còn lại
+ Cài đặt:
=> Exchange(a,m, m+k, i): hoán đổi i pt lần lượt từ m<-> m+k ...
CHƯƠNG 5: Giải thuật Tham lam
I Giới thiệu
+ thường dùng trong các bài toán tối ưu tổ hợp ròi rạc dạng min{f(x): x thuộc D} D là tập hữu hạn rời rạc
+ Phương pháp tham lam chỉ đưa ra kết quả tốt( ko tối ưu) trong thời gian nhanh chóng
+ Ý tưởng: xuất phát từ lời giải rỗng
Trong đó:
II Bài toán cái túi (Knapshap)
+ Có n đồ vật: đồ vật thứ i có trọng lượng wi, giá trị ci, trọng lượng tối đa của túi b=> láy đồ vật với đk: tổng kl< =b, giá trị max nhất
+ Giải: 1, Giá tri lớn nhất thì lấy
2, Trọng lượng nhỏ nhất thì lấy
3, giá tri/trọng lượng ( đơn giá) nhỏ nhất thì lấy
III Bài toán người du lịch
+ Đường đi ngắn nhất khi đi qua n thành phố
+ Giải: 1,chọn thành phố gần nhất với thành phố hiện thời
IV Bài toán đường đi ngắn nhất
+ cho G(V,E): tìm đường đi ngắn nhất từ s0 đến các đỉnh còn lại
+ Thuật toán Dijkstra:
=> đi từ đỉnh s0( thuộc S), tính giá trị từ s0=> các đỉnh còn lại chọn đỉnh min(gán luôn nhãn min vào đỉnh đó) => vd là s1 đưa vào S, ... Tiếp tục xét các đỉnh lân cận với s0,s1 ( thuộc S), => chọn min => đưa S .... tiếp tục cho đến khi tập S bằng tập đỉnh ban đầu
+ Ví dụ:
+ Cài đặt:
V Bài toán cây bao trùm nhỏ nhất (MST)
+ Cây là đồ thị không có chù trình
+ Chu trình là đường đi từ 1 đỉnh về lại chính nó
+ Cây bao trùm là cây đi qua tất cả các đỉnh
ứng dụng: bt nối dây điện cho mạch nối tiếp, => tốn ít nhất
=> bài toán đơn giản trở thành tìm đường đi ngắn nhất không tạo thành chu trình
+ Thuật toán Prim:
=> Ta sẽ lấy 1 đỉnh bất kì làm đỉnh gốc, tìm cạnh( bản chất tìm đỉnh kề ) có trọng số nhỏ nhất.... như thuật toán đường đi nn
+ Thuật toán Kruskal:
=> Khác với thuật toán Prim: Kruskal sẽ cho luôn n đỉnh ban đầu, và tìm cách nối các đỉnh thành các cạnh (có n-1) .... chọn các cảnh từ nhỏ => lớn với điều kiện: không chu trình,,,,,
Ban đầu sẽ có n cây( n đỉnh),, chọn cạnh từ nhỏ nhất , các cạnh nối với nhau tạo thành 1 cây,,, chọn các cạnh đến khi chỉ còn 1 cây,,,
VI Bài toán Tô màu
+ tô màu tất cả các đỉnh của đồ thị sao cho không có 2 đỉnh nào kề nhau có cùng màu với số màu ít nhất
vd: xếp lịch học cho một trường học, không có sinh viên nào học trùng môn tại 1 thời điểm
+ Ý tưởng : quy ước các màu là các số 1,2,3,...
b1: tô đỉnh bất kỳ màu 1
b2: với đỉnh chưa tô: tô nó với màu nhỏ nhất so với các đỉnh kề đã đk tô màu.... lặp lại bước này cho đến khi tô hết các đỉnh
=> thứ tự tô khác nhau sẽ có số lượng màu cần dùng khác nhau
VII Bài toán tìm các khoảng không giao nhau
+ có n công việc cần thực hiện: ai: thời gian bắt đầu, bi: tg kết thúc công việc thứ i... chọn ra các việc nhiều nhất mà 1 người có thể làm
+Ý tưởng: C là tập ban đầu, S là tập công việc lựa chọn...
1, Sắp xếp các việc theo thứ tự tăng dần của đầu mút trái ai,,,,,
2, Lần lượt xét các công việc này: chọn cv thỏa mãn giao với S = rỗng
+ Ý tưởng 2: chọn (bi-ai) nhỏ nhất trước
+ Ý tưởng 3: chọn bi nhỏ nhất trước
Bài 9,10: Quy hoạch động
+ bài toán fibonaci đối với chia để trị, chúng ta sẽ phải thực hiện các bài toán con nhiều lần
=> Quy hoạch động
+ đặc điểm: chia bt lớn thành các bt con=> tổng hợp lại; lưu trữ kq của các bt con để sử dụng lại(mảng,..); (tiếp cận từ dưới lên)
1 bài toán fibonaci: dùng mảng lưu lại các giá trị từ nhỏ đến ...
2 bt Cái túi: (đk: trọng lượng phải nguyên)
+ n: số đồ vật; b: trọng lượng túi; i: 0->n; L: 0->b;
+ MaxV(i,L): bài toán con với số đồ vật từ 0->i, tl túi là L
=> MaxV(n,b): lời giải bài toán cần tìm
+ Thuật toán: MaxV(0,L)= MaxV(i,0)=0; với mọi L,i
B1: giả sử có MaxV(i-1,L) => tính MaxV(i,L)
B2: xét đồ vật thứ i khi trọng lượng túi vẫn là L
MaxV(i,L) = Max{MaxV(i-1,L-w(i))+ c[i], MaxV(i-1,L)}
+ Độ phức tạp O(n*b)
3 bt Dãy con có tổng lớn nhất
+ MaxS[i]: tổng lớn nhất của dãy con từ a1-> ai
+ MaxS[N]: giá trị cần tìm
+ MaxS[1]= a[1]
+ MaxE[i]: tổng lớn nhất tạm thời
+ Khi tăng i: 2 trường hợp: dãy cần tìm chứa a[i], không chứa a[i]
Th1: MaxE[i]= MaxE[i-1]+ a[i]
Th2: MaxE[i]= a[i]
5 Bài toán tìm xâu con chung dài nhất
=> chú ý về cách sắp xếp mảng:
6 Đường đi ngắn nhất TT Floyd
+ Ví dụ:
+ Cài đặt:
+ Thuật toán tìm cây nhị phân tìm kiếm tối ưu
Thuật toán quay lui
1 Bài toán 8 con hậu: xếp 8 con hậu trên bàn cờ vua sao cho chúng không ăn nhau
2 Bài toán ngựa đi tuần
I Giới thiệu
+ thuật toán:
1, kn: 1 loạt bước thực hiện bài toán( để từ input=> ouput đúng)
2, tc: chính xác, rõ ràng, khách quan, phổ dụng, kết thúc
3, bd: NN tự nhiên, sơ đồ khối, giả mã(phải mô tả đk cả input,output)
4, chất lượng bd: đúng; đơn giản; dễ cài đặt
5, Chứng minh tính đúng đắn: pp lý thuyết, thực nghiệm
6, Tính hiệu quả: thời gian, bộ nhớ, độ chính xác
+ Đánh giá độ phức tạp:
1, độ tăng của hàm: ham O (lớn) : tc: quy tắc cộng, quy tắc nhân
2, độ .. thời gian: hàm f(n): đếm số phép toán cơ bản: gán, so sánh,.. ( n là kích thước dữ liệu đầu vào): độ phức tạp là hàm chặn trên O của nó
+ Lớp P: lớp các bt giải đk bằng tg đa thức
+ Lớp NP: ......... kiểm tra tính đúng của lời giải bằng tg đa thức
-> những bài toán NP có thể là bt P được không?
+ 1 số quy tắc đánh giá: quy tắc cộng( max( 2 hàm)), quy tắc nhân( tích độ phức tạp 2 hàm), phân tích câu lệnh,,,,
+ Phương pháp đánh giá:
1 phân tích trực tiếp các đoạn mã (đếm , đếm, đếm)
2 .............. lý thuyết
3 ............. thực nghiệm
2: thực hiện 2 việc: cm tính đúng, cm tính hiệu quả(****)
+ ví dụ: phương pháp Merge sort : sử dụng Tree để phân tích
+ chương trính hóa thuật toán
+ các lệnh đếm các phép toán
+ chạy chương trình trên nhiều bộ DL sẵn có
=> mỗi bộ ghi lại kết quả=> thống kê
Bài 3: Thiết kế thuật toán
1 Kn: là module hóa bài toán ban đầu thành các vấn đề nhỏ, cố gắng giải quyết tốt các vấn đề nhỏ đó => gom => giải quyết bt lớn
2 Một số kỹ thuật thiết kế
+ Chia để trị: chia thành đoạn hoặc bài toán nhỏ hơn
+ Tham lam: Chọn phương án tốt hiện thời(tốc độ nhanh, nhưng..)
+ Quy hoạch động: nhanh, kq tối ưu nhưng bộ nhớ lớn
+ Quay Lui: thử => sai => sủa
+ Nhánh cận: bc là quay lui + đánh giá cận và cắt bớt nếu ko cần
3 Tối ưu thuật toán
+ tối ưu thuật toán + thay đổi cấu trúc dữ liệu
+ Thay đổi kỹ thuật, công nghệ
+ tối ưu vòng lặp
Bài 4: chia để trị
Ý tưởng: chia bài toán => các bt con độc lập( về biên dữ liệu) vs nhau, giải bt con theo cùng 1 cách thức=> tổng hợp lại
1 Tìm kiếm nhị phân
+ Input: mảng A có n phần tử đã được sắp xếp theo thứ tự tăng dần, tìm phần tử có giá trị = X trong mảng =>
+ Output: k=-1 nếu không tìm thấy,,, 1<=k<=n nếu tìm thấy
+ Ý tưởng: lấy k= (left + right)/2 kiểm tra A[k] = X return k; nếu A[k]> X thì tiếp tục chia trên mảng left-> k-1; A[k]<X : tiếp tục chia trên: k+1 đến right
+ Cài đặt:
=> độ phức tạp O(log2(n))
2 Bài toán tìm Max và min
+ Input: mảng A có n phần tử
+ Output: giá trị lớn nhất, nhỏ nhất trong mảng A
+ Ý tưởng: chia đôi mảng A, tìm min, max trên mỗi nửa, rồi tổng hợp lại,, nếu mảng còn 1 phần tử thì min=max=phần tử đó
+ Cài đặt:
3 Bt Merge Sort
+ Input: mảng A có n phần tử
+ Output: mảng A có n phần tử đã được sắp xếp tăng dần
+ Ý tưởng:
nếu có 2 dãy a,b đã đk sắp xếp=> trộn thành dãy c đk sắp xếp
chia nhỏ mỗi dãy chỉ còn 1 phần tử => trộn lại vs nhau
+ Cài đặt mergesort:
4 Quick Sort
+ Input: mảng A có n phần tử
+ Output: mảng A đã được sắp xếp tăng dần
+ Ý tưởng: lấy mỗi phần tử và chuyển nó đến vị trí đúng
+ Cài đặt phân đoạn Partition :
Chọn phần tử chôt x:
• Duyệt từ vị trí tiếp sang phải tìm vị trí phần tử đầu tiên >= x, i• Duyệt từ phải sang trái, tìm vị trí phần tử đầu tiên <x, j• Nếu i<j thì hoán đổi vị trí• Tiếp tục đến lúc j<i
+ Cài đặt quicksort:
5 Bài toán nhân số nguyên lớn
+ Input: 2 số nguyên lớn x,y có n chữ số
+ Output: số nguyên lớn z = x.y
+ Ý tưởng:
=> độ phức tạp O(n^2) không nhanh hơn bình thường
+ Ý tưởng thuật toán Karatsuba
+ Cài đặt karatsuba
6 Nhân ma trận
+ Input: 2 ma tran X(m,n) và Y(n,p)
+ Output: ma trận Z= tích của X và Y
+ Ý tưởng: chia X thành 4 mt con A,B,C,D ; Y thành 4 mt con E,F,G,H
=> Strassen: đặt
P1= A(F-H) P2= (A+B)H P3= (C+D)E P4= D(G-E)
P5= (A+D)(E+H) P6= (B-D)(G+H) P7= (A-C)(E+F)
7 Dãy con lớn nhất
+ Input: mảng A[1...n]
+ Output: mảng A[p...q] có trọng lượng( tổng giá trị các pt) lớn nhất, p-> q là liên tiếp 1<=p<=q<= n
+ Ý tưởng: chia mảng A thành 2 mảng đều: AL, AR
tính WL: trọng lượng (dãy con) max thuộc mảng AL
WR: trọng lượng (dãy con) max thuộc mảng AR
WM: trọng lượng (dãy con) max thuộc mảng AL,AR xuất phát tại điểm chính giữa AL ,AR => Max= Max(WL,WR,WM)
+ Cài đặt:
8 Tính lũy thừa
+ Tính a^n với a,n là số nguyên ko âm
+ Ý tưởng:
=> độ phức tạp O(log(n))
+ cài đặt:
9 Hoán đổi phần tử mảng
+ Input: mảng A có n phần tử
+ Output: mảng A sau khi chuyển m phần tử đầu về cuối với đk không dùng mảng phụ
+ Ý tưởng:
1, Nếu m=n-m: hoán đổi 2 mảng có độ dài bằng nhau
2, Nếu m<n-m: .............. m pt đầu vs m pt cuối => còn A[1..n-m]
cần chuyển đúng vị trí: tt hoán đổi m pt đầu vs phần còn lại
3, Nếu m>n-m: ............(n-m) phần tử đầu về cuối->.A[n-m+1...n]
cần...........................: ta hoán đổi (n-m) pt đầu vs phần còn lại
+ Cài đặt:
CHƯƠNG 5: Giải thuật Tham lam
I Giới thiệu
+ thường dùng trong các bài toán tối ưu tổ hợp ròi rạc dạng min{f(x): x thuộc D} D là tập hữu hạn rời rạc
+ Phương pháp tham lam chỉ đưa ra kết quả tốt( ko tối ưu) trong thời gian nhanh chóng
+ Ý tưởng: xuất phát từ lời giải rỗng
II Bài toán cái túi (Knapshap)
+ Có n đồ vật: đồ vật thứ i có trọng lượng wi, giá trị ci, trọng lượng tối đa của túi b=> láy đồ vật với đk: tổng kl< =b, giá trị max nhất
+ Giải: 1, Giá tri lớn nhất thì lấy
2, Trọng lượng nhỏ nhất thì lấy
3, giá tri/trọng lượng ( đơn giá) nhỏ nhất thì lấy
III Bài toán người du lịch
+ Đường đi ngắn nhất khi đi qua n thành phố
+ Giải: 1,chọn thành phố gần nhất với thành phố hiện thời
IV Bài toán đường đi ngắn nhất
+ cho G(V,E): tìm đường đi ngắn nhất từ s0 đến các đỉnh còn lại
+ Thuật toán Dijkstra:
=> đi từ đỉnh s0( thuộc S), tính giá trị từ s0=> các đỉnh còn lại chọn đỉnh min(gán luôn nhãn min vào đỉnh đó) => vd là s1 đưa vào S, ... Tiếp tục xét các đỉnh lân cận với s0,s1 ( thuộc S), => chọn min => đưa S .... tiếp tục cho đến khi tập S bằng tập đỉnh ban đầu
+ Cài đặt:
V Bài toán cây bao trùm nhỏ nhất (MST)
+ Cây là đồ thị không có chù trình
+ Chu trình là đường đi từ 1 đỉnh về lại chính nó
+ Cây bao trùm là cây đi qua tất cả các đỉnh
ứng dụng: bt nối dây điện cho mạch nối tiếp, => tốn ít nhất
+ Thuật toán Prim:
+ Thuật toán Kruskal:
Ban đầu sẽ có n cây( n đỉnh),, chọn cạnh từ nhỏ nhất , các cạnh nối với nhau tạo thành 1 cây,,, chọn các cạnh đến khi chỉ còn 1 cây,,,
VI Bài toán Tô màu
+ tô màu tất cả các đỉnh của đồ thị sao cho không có 2 đỉnh nào kề nhau có cùng màu với số màu ít nhất
vd: xếp lịch học cho một trường học, không có sinh viên nào học trùng môn tại 1 thời điểm
+ Ý tưởng : quy ước các màu là các số 1,2,3,...
b1: tô đỉnh bất kỳ màu 1
b2: với đỉnh chưa tô: tô nó với màu nhỏ nhất so với các đỉnh kề đã đk tô màu.... lặp lại bước này cho đến khi tô hết các đỉnh
=> thứ tự tô khác nhau sẽ có số lượng màu cần dùng khác nhau
VII Bài toán tìm các khoảng không giao nhau
+ có n công việc cần thực hiện: ai: thời gian bắt đầu, bi: tg kết thúc công việc thứ i... chọn ra các việc nhiều nhất mà 1 người có thể làm
+Ý tưởng: C là tập ban đầu, S là tập công việc lựa chọn...
1, Sắp xếp các việc theo thứ tự tăng dần của đầu mút trái ai,,,,,
2, Lần lượt xét các công việc này: chọn cv thỏa mãn giao với S = rỗng
+ Ý tưởng 2: chọn (bi-ai) nhỏ nhất trước
+ Ý tưởng 3: chọn bi nhỏ nhất trước
Bài 9,10: Quy hoạch động
+ bài toán fibonaci đối với chia để trị, chúng ta sẽ phải thực hiện các bài toán con nhiều lần
=> Quy hoạch động
+ đặc điểm: chia bt lớn thành các bt con=> tổng hợp lại; lưu trữ kq của các bt con để sử dụng lại(mảng,..); (tiếp cận từ dưới lên)
1 bài toán fibonaci: dùng mảng lưu lại các giá trị từ nhỏ đến ...
2 bt Cái túi: (đk: trọng lượng phải nguyên)
+ n: số đồ vật; b: trọng lượng túi; i: 0->n; L: 0->b;
+ MaxV(i,L): bài toán con với số đồ vật từ 0->i, tl túi là L
=> MaxV(n,b): lời giải bài toán cần tìm
+ Thuật toán: MaxV(0,L)= MaxV(i,0)=0; với mọi L,i
B1: giả sử có MaxV(i-1,L) => tính MaxV(i,L)
B2: xét đồ vật thứ i khi trọng lượng túi vẫn là L
MaxV(i,L) = Max{MaxV(i-1,L-w(i))+ c[i], MaxV(i-1,L)}
+ Độ phức tạp O(n*b)
3 bt Dãy con có tổng lớn nhất
+ MaxS[i]: tổng lớn nhất của dãy con từ a1-> ai
+ MaxS[N]: giá trị cần tìm
+ MaxS[1]= a[1]
+ MaxE[i]: tổng lớn nhất tạm thời
+ Khi tăng i: 2 trường hợp: dãy cần tìm chứa a[i], không chứa a[i]
Th1: MaxE[i]= MaxE[i-1]+ a[i]
Th2: MaxE[i]= a[i]
5 Bài toán tìm xâu con chung dài nhất
6 Đường đi ngắn nhất TT Floyd
+ Cài đặt:
+ Thuật toán tìm cây nhị phân tìm kiếm tối ưu
Thuật toán quay lui
1 Bài toán 8 con hậu: xếp 8 con hậu trên bàn cờ vua sao cho chúng không ăn nhau
2 Bài toán ngựa đi tuần
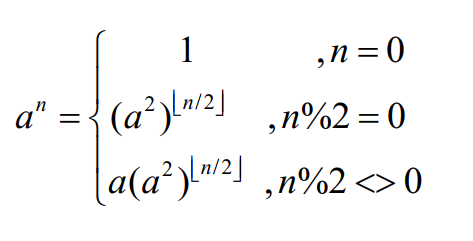
Nhận xét
Đăng nhận xét